Phase-field approaches in Topology Optimization

In a Topology Optimization problem, we often have a design variable in [-1, 1], representing how much material do we place at each point. A formal presentation of the problem is as follows

Alternatively, we can create an evolution equation for , such that the evolution process is equivalent with the above optimization process. In phase-field modeling, we have an evolution equation (either Allen-Cahn or Cahn-Hilliard type), and the goal is to minimize free energy. To solve the current Topology Optimization with phase-field modeling strategy, we adjust the free energy by adding the cost function. The volume constraint is accounted via a penalty term inspired by the augmented Lagrangian. So the equivalent evolution equation can be written as

Here, the math seems a little bit overwhelming, but the evolution equation is simply a diffusion-reaction equation (also an Allen-Cahn equation). The source term is composed of the double-well function (commonly used in phase-field), the cost function, and the penalty of volume contraint. The coefficients are adjustable variables that control the driving force of each piece of the evolution equation.

Now we only miss the PDE constraint. This is accomplished by a sensitivity analysis (adjoint problem). The derivation of ajoint problem is skipped here. A good reference is dofin-adjoint documentation.

algorithm

The full solving algorithm is presented as follows.

This algorithm is implemented in an open-source code FEniCS.

simulation examples

The first working example is a standard one, namely optimization the compliance of a cantilever beam. Various tests are carried out for this simple case to validate the algorithm and clarify the coefficient parameters.

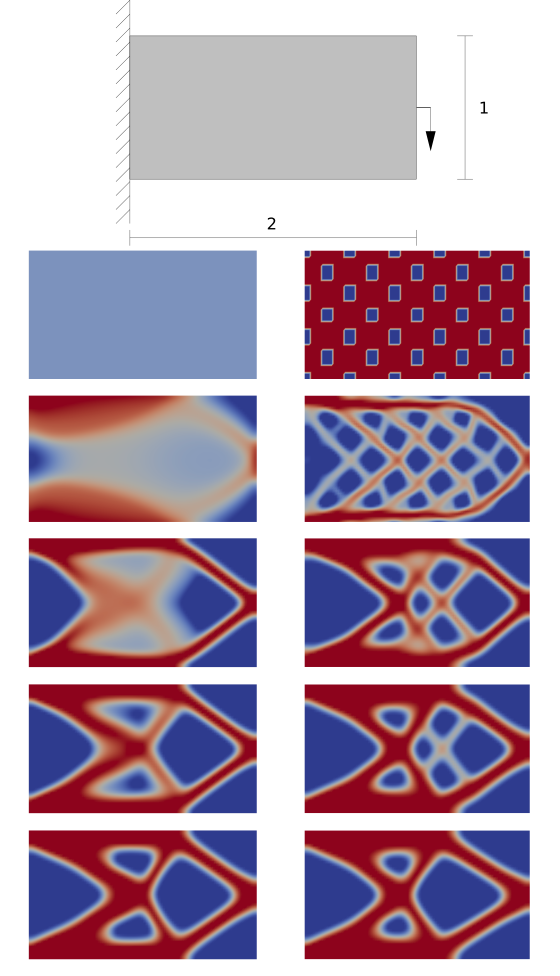
The solution in 3D is also possible. Finer mesh ends with geometry with more details.

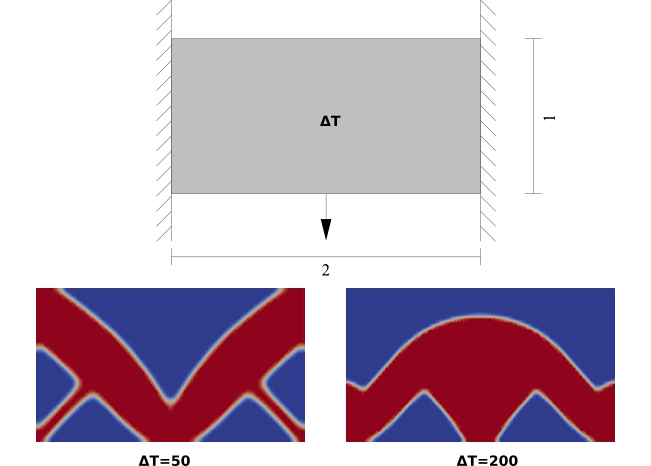
We can also solve a therm-mechanical problem presented below. We observe a significant geometry change due to the increase of temperature change. In other words, if the structure expansion is magnified, we need a thicker lower strut to maintain the stiffness. This result is consistent with the result in literature.

my master thesis